Egy egyszerű eset szemléltetéséhez vegyünk egy olyan példát, amikor a reakció során 'A' anyag 'B' anyaggá alakul át (A
 B). A reakciósebességet (
B). A reakciósebességet (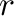 ) a koncentrációk idő szerinti differenciálhányadosaként írhatjuk fel:
) a koncentrációk idő szerinti differenciálhányadosaként írhatjuk fel:
![$\displaystyle r=-\frac{d[\mathrm{A}]}{dt}=\frac{d[\mathrm{B}]}{dt}$](img76.png) |
(4.5) |
Az egyenletben 'A' anyag koncentrációja negatív, míg a 'B' anyagé pozitív előjellel szerepel, mivel a reakció során az utóbbi mennyisége növekszik az előbbi rovására. Az 'A'-ra felírt reakcósebesség kifejezhető a koncentráció és a (jelen esetben elsőrendű) sebességi állandó szorzataként:
![$\displaystyle -r_A=k[\mathrm{A}] ~~ \left[\frac{\mathrm{mol}}{\mathrm{l} \cdot \mathrm{s}} \right]$](img77.png) |
(4.6) |
Előfordulnak olyan reakciók is, amikor a reakciósebesség egyáltalán nem függ a reaktánsok koncentrációjától. Ilyen például az az eset, amikor a hidrogén és klór gázok fénybesugárzás hatására sósavgázzá alakulnak. Ha az 4.5 egyenletet integráljuk, akkor koncentrációra a következő összefüggést kapjuk:
![$\displaystyle [\mathrm{A}]=-kt+\mathrm{konstans}$](img78.png) |
(4.7) |
A kezdeti feltétel ( esetén
esetén
![$[\mathrm{A}]=[\mathrm{A_0}]$](img80.png) ) figyelembe vételével a koncentráció-idő összefüggés az alábbi módon alakul:
) figyelembe vételével a koncentráció-idő összefüggés az alábbi módon alakul:
![$\displaystyle [A]=-kt+[A_0]$](img81.png) |
(4.8) |
Azaz, egy egyenes egyenletét kapjuk, ahol a sebességi állandó (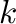 ) a meredekség, míg a kezdeti koncentráció (
) a meredekség, míg a kezdeti koncentráció (
![$[\mathrm{A_0}]$](img82.png) ) a metszéspont.
) a metszéspont.
Nézzünk egy elsőrendű reakciót, ahol 'A' anyagból 'B' és 'C' lesz (A
 B + C). Kezdeti feltételként ismerjük a koncentrációkat:
B + C). Kezdeti feltételként ismerjük a koncentrációkat:
![$[\mathrm{A}]_0=a$](img83.png) ;
;
![$[\mathrm{B}]_0=[\mathrm{C}]_0=0$](img84.png) . Ha
. Ha 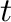 idő múlva
idő múlva 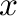 mól 'A' elreagál, akkor a koncentrációk a következők lesznek:
mól 'A' elreagál, akkor a koncentrációk a következők lesznek:
![$\displaystyle [\mathrm{A}]=(a-x) ~~~~~~~~~ [\mathrm{B}]=[\mathrm{C}]=x$](img87.png) |
(4.9) |
Ha 'A' átalakulására elsőrendű reakciót feltételezünk, akkor a sebesség a következő lesz:
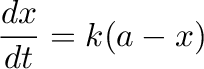 |
(4.10) |
A 4.10 egyenletet integrálva a következő egyenletet kapjuk:
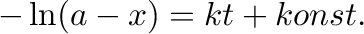 |
(4.11) |
A kezdeti feltételeket figyelembe véve ( ,
, 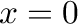 ) a konstans értéke
) a konstans értéke 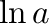 lesz. Így az egyenletünk a következőképpen alakul:
lesz. Így az egyenletünk a következőképpen alakul:
 |
(4.12) |
vagy ha bevezetjük a konverzió fogalmát és  -val jelöljük:
-val jelöljük:
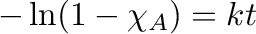 |
(4.13) |
Elsőrendű reakció esetén, ha a
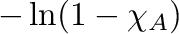 kifejezést ábrázoljuk
kifejezést ábrázoljuk 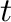 függvényében, akkor egy
függvényében, akkor egy 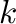 meredekségű egyeneshez jutunk.
meredekségű egyeneshez jutunk.
Nézzünk egy addíciós reakciót, ahol 'A' és 'B' kiindulási anyagokból 'C' terméket kapjuk (A + B
 C). A reakciósebesség ebben az esetben függeni fog mindkét reaktáns koncentrációjától:
C). A reakciósebesség ebben az esetben függeni fog mindkét reaktáns koncentrációjától:
![$\displaystyle r=k[\mathrm{A}][\mathrm{B}]$](img96.png) |
(4.14) |
Fontos megjegyezni, hogy a 4.14 egyenletben szereplő 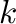 nem hasonlítható össze egy elsőrendű reakció sebességi állandójával! Elsőrendű esetben ugyanis
nem hasonlítható össze egy elsőrendű reakció sebességi állandójával! Elsőrendű esetben ugyanis 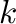 dimenziója [idő]
dimenziója [idő] , míg másodrendű reakciónál az állandó mértékegysége [idő]
, míg másodrendű reakciónál az állandó mértékegysége [idő] [koncentráció]
[koncentráció] . Igazából még egy ugyanolyan másodrendű katalitikus és nemkatalitikus reakció sebességi állandóit sem lehet egymáshoz méricskélni. Katalitikus esetben ugyanis a sebesség nagy valószínűséggel függeni fog a katalizátor koncentrációjától, és a hatványkitevőkben az egyes komponensek részrendjei fognak megjelenni:
. Igazából még egy ugyanolyan másodrendű katalitikus és nemkatalitikus reakció sebességi állandóit sem lehet egymáshoz méricskélni. Katalitikus esetben ugyanis a sebesség nagy valószínűséggel függeni fog a katalizátor koncentrációjától, és a hatványkitevőkben az egyes komponensek részrendjei fognak megjelenni:
![$\displaystyle r=k[kat.]^\alpha[\mathrm{A}]^\beta[\mathrm{B}]^\gamma$](img97.png) |
(4.15) |
 B). A reakciósebességet (
B). A reakciósebességet (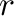 ) a koncentrációk idő szerinti differenciálhányadosaként írhatjuk fel:
) a koncentrációk idő szerinti differenciálhányadosaként írhatjuk fel:
 B). A reakciósebességet (
B). A reakciósebességet (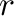 ) a koncentrációk idő szerinti differenciálhányadosaként írhatjuk fel:
) a koncentrációk idő szerinti differenciálhányadosaként írhatjuk fel:
![$\displaystyle -r_A=k[\mathrm{A}] ~~ \left[\frac{\mathrm{mol}}{\mathrm{l} \cdot \mathrm{s}} \right]$](img77.png)
![$\displaystyle [\mathrm{A}]=-kt+\mathrm{konstans}$](img78.png)
 esetén
esetén
![$[\mathrm{A}]=[\mathrm{A_0}]$](img80.png) ) figyelembe vételével a koncentráció-idő összefüggés az alábbi módon alakul:
) figyelembe vételével a koncentráció-idő összefüggés az alábbi módon alakul:
![$\displaystyle [A]=-kt+[A_0]$](img81.png)
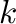 ) a meredekség, míg a kezdeti koncentráció (
) a meredekség, míg a kezdeti koncentráció (
![$[\mathrm{A_0}]$](img82.png) ) a metszéspont.
) a metszéspont.
 B + C). Kezdeti feltételként ismerjük a koncentrációkat:
B + C). Kezdeti feltételként ismerjük a koncentrációkat:
![$[\mathrm{A}]_0=a$](img83.png) ;
;
![$[\mathrm{B}]_0=[\mathrm{C}]_0=0$](img84.png) . Ha
. Ha 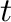 idő múlva
idő múlva 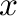 mól 'A' elreagál, akkor a koncentrációk a következők lesznek:
mól 'A' elreagál, akkor a koncentrációk a következők lesznek:
![$\displaystyle [\mathrm{A}]=(a-x) ~~~~~~~~~ [\mathrm{B}]=[\mathrm{C}]=x$](img87.png)
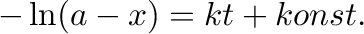
 ,
, 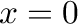 ) a konstans értéke
) a konstans értéke 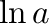 lesz. Így az egyenletünk a következőképpen alakul:
lesz. Így az egyenletünk a következőképpen alakul:

 -val jelöljük:
-val jelöljük:
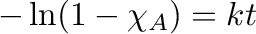
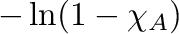 kifejezést ábrázoljuk
kifejezést ábrázoljuk 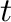 függvényében, akkor egy
függvényében, akkor egy 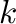 meredekségű egyeneshez jutunk.
meredekségű egyeneshez jutunk.
 C). A reakciósebesség ebben az esetben függeni fog mindkét reaktáns koncentrációjától:
C). A reakciósebesség ebben az esetben függeni fog mindkét reaktáns koncentrációjától:
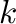 nem hasonlítható össze egy elsőrendű reakció sebességi állandójával! Elsőrendű esetben ugyanis
nem hasonlítható össze egy elsőrendű reakció sebességi állandójával! Elsőrendű esetben ugyanis 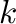 dimenziója [idő]
dimenziója [idő] , míg másodrendű reakciónál az állandó mértékegysége [idő]
, míg másodrendű reakciónál az állandó mértékegysége [idő] [koncentráció]
[koncentráció] . Igazából még egy ugyanolyan másodrendű katalitikus és nemkatalitikus reakció sebességi állandóit sem lehet egymáshoz méricskélni. Katalitikus esetben ugyanis a sebesség nagy valószínűséggel függeni fog a katalizátor koncentrációjától, és a hatványkitevőkben az egyes komponensek részrendjei fognak megjelenni:
. Igazából még egy ugyanolyan másodrendű katalitikus és nemkatalitikus reakció sebességi állandóit sem lehet egymáshoz méricskélni. Katalitikus esetben ugyanis a sebesség nagy valószínűséggel függeni fog a katalizátor koncentrációjától, és a hatványkitevőkben az egyes komponensek részrendjei fognak megjelenni:
![$\displaystyle r=k[kat.]^\alpha[\mathrm{A}]^\beta[\mathrm{B}]^\gamma$](img97.png)