Kinetika és katalízis

Mielőtt a matematikai/fizikai alapokat megtekintenénk, tegyünk gondolatban egy kirándulást egy dimbes-dombos vidéken, ahol A pontból el kell jutnunk B pontba. A kiindulási és célállomás adott, ezeken nem tudunk változtatni. Adott ezeknek a tengerszint feletti magassága is, tehát a szintkülönbség, amivel alacsonyabban (vagy magasabban) leszünk az út végén az tisztán attól függ, hogy honnan hová akarunk eljutni. Az viszont már tőlünk függ, hogy a több lehetséges útvonal közül, melyek völgyeken és hágókon át vezetnek, melyiket választjuk ki (4.1 ábra).

4.1. Ábra: Domborzati ábrázolás két lehetséges útvonallal, mely a lehető legkisebb magasságon próbál eljutni A pontból B pontba.

Ami a katalitikus reakciókat illeti, szinte pontosan ugyanez a helyzet, ha A-ból B-be kell eljutnunk, azaz adottak a kiindulási anyagok és adottak a termékek. Tengerszint feletti magasság helyett itt persze a szintvonalak közvetlenül jelentenek energia értékeket. Megjegyzendő, hogy a reakciútvonalak ilyesfajta ábrázolása a Born-Oppenheimer közelítés alkalmazásával képzelhető el, melynek lényege, hogy a molekulák kvantummechanikai leírásában elkülöníti az elektronok és az atommagok mozgását, mivel az atommagok tömege sokkal nagyobb, mint az elektronoké. Ennek köszönhetően az atommagok mozgása lassúbb, így az elektronok mozgását a kvázi-stacionárius atommagok körül vizsgálhatjuk. Ezáltal egy potenciálenergia-felületet (PES) kapunk, amely az atommagok különböző konfigurációihoz tartozó elektronenergiákat ábrázolja. A PES használatával egyszerűbbé válik a kémiai reakciók leírása, mivel a reakcióútvonalakat, a kiindulási anyagokat, a termékeket, a közti termékeket és az átmeneti állapotokat ezen a felületen ábrázolhatjuk, így részletesebb képet kapunk a reakciómechanizmusokról és az energiaprofilról. Természetesen a domborzati analógiánál a PES esetében némileg bonyolultabb a helyzet, ugyanis ott a tengerszint feletti magasságot ábrázoljuk a két másik helykoordináta függvényében, itt viszont az energiafüggvény változóinak száma mindenképpen több, mint kettő (hacsak nem kétatomos molekuláról van szó); ha 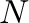$N$ az atomok száma, akkor 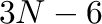$3N-6$ változós függvényünk van (lineáris molekulánál 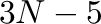$3N-5$). Az összes szabadsági fokból levonásra kerülnek a transzlációs és rotációs szabadsági fokok, azaz azok, amikor az összes atom egymáshoz képes egy irányba mozdul el, és azok is, amikor a háromdimenziós tér három tengelye körül forgatjuk el az összes atomot egyszerre, úgy hogy az egymáshoz viszonyított pozíciójuk nem változik. Így aztán a PES korrektebb elnevezése potenciálenergia hiperfelület, amit az Euklideszi térben értelmezünk.

Gyakorlati szempontból meglehetősen nehéz (sőt lehetetlen) lenne a reakcióútvonalakat háromnál több dimenzióban ábrázolni, ezért be szokták vezetni a reakciókoordináta fogalmát, mely a teljes útvonal kétdimenziós metszete. Itt már könnyedén meg lehet jeleníteni a potenciálenergia hiperfelület kiemelt pontjait, azaz az átmeneti állapotokat és a közti termékeket.

A termodinamikai egyensúly tehát adott, azaz a termékek és a kiindulási anyagok szabadentalpiái közötti különbség magának a reakciónak egy olyan alapvető tulajdonsága, amire nincs ráhatásunk. Körülbelül 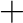$+$40 kJ/mol az a reakciószabadentalpia, aminél ha nagyobb a tervezett reakciónkra előzetesen kalkulált 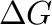$\Delta G$, akkor azon semmiféle katalizátor nem fog segíteni.^4.1Ha a termodinamika nem húzza keresztül a számításunkat, akkor viszont arra van befolyásunk (persze sokszor csak elvben), hogy kiválasszuk a megfelelő katalizátort, azaz eldöntsük, hogy többféle lehetséges útvonal közül melyiket járjuk végig a kezdeti és a végállapot között.

A kémiai reakció sebességi állandójának hőmérsékletfüggését az Arrhenius-egyenlet írja le. Az egyenlet alapvető összetevői az aktiválási energia, (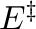$E^\ddag$ vagy néha 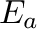$E_a$), a preexponenciális faktor, (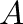$A$), az egyetemes gázállandó, (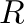$R$), és az abszolút hőmérséklet (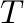$T$). Az egyenlet azt mutatja, hogy a reakciósebességek nőnek a hőmérséklettel, ahogy a reagensek megkapják a sikeres reakcióhoz szükséges aktiválási energiát:

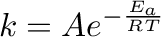$$k=Ae^{-\frac{E_a}{RT}}$$ (4.1)

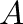Az Arrhenius-egyenlet segítséget nyújt a reakciósebességek előrejelzéséhez és az energiaprofilok interpretálásához, noha sokan kritikával illetik a leegyszerűsítő ábrázolásmódja miatt. Nehezen megfogható mennyiség ugyanis az $A$ preexponenciális faktor, mivel nincs egyértelmű fizikai definíciója. Ami a dimenzióját illeti, annak egyeznie kell a sebességi állandó dimenziójával (pl. 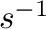$s^{-1}$ egy elsőrendű reakció esetén), mivel ez exponenciális tag dimenziómentes szám. Megemlítendő, hogy nagyon kis aktiválási energiák esetén (kb. 20 kJ/mol alatt) már nem annyira a reakciómechanizmussal kapcsolatos kémiai folyamatok a meghatározók, hanem a részecskék közötti kölcsönhatás sebessége. Az ilyen eseteket diffúziókontrollált folyamatoknak nevezzük.

Az aktiválási paraméterek, mint az entalpia, entrópia és térfogat, kulcsfontosságúak a kinetika és a reakciómechanizmusok értelmezésében. Ezek a paraméterek az elemi reakciók esetében meghatározhatók, és segítenek a többlépcsős reakciók egyes lépéseinek elemzésében. Maga az aktiválás az a folyamat, amikor a reaktánsok szert tesznek arra az extra energiára, ami elegendő ahhoz, hogy el tudjanak jutni az átmeneti állapotig. Az energia nem egyenletesen oszlik el a részecskék között; egy részük energiája viszont meghaladja az aktiválási energiát. A statisztikus termodinamikában a Boltzmann eloszlás segítségével lehet kiszámolni az adott energiaszintet meghaladó populáció arányát. A Boltzmann eloszlás lényege a hőmérsékletet a nevezőben tartalmazó exponenciális tag, 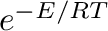$e^{-E/RT}$, ami hangsúlyos része az Arrhenius egyenletnek is.

Az Eyring-egyenlet elsősorban a kémiai reakciók sebességállandójának hőmérsékletfüggését írja le. Ez egy alapvető fontosságú képlet a reakciókinetikában, mely arra szolgál, hogy meghatározza, hogyan változik egy reakció sebessége a hőmérséklet függvényében.

$$k=\frac{\kappa k_BT}{h}e^{-\Delta G^\ddag /RT}$$ (4.2)

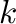ahol $k$ a sebességi állandó, 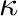$\kappa$ a transzmissziós koefficiens (értéke többnyire 1), 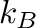$k_B$ a Boltzmann állandó, 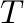$T$ a hőmérséklet, 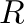$R$ az egyetemes gázállandó, 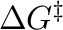$\Delta G^\ddag$ pedig az aktiválási szabadentalpia.

A képlet igen hasznosnak bizonyul a kémiai reakciók dinamikájának megértésében, és úgyszolván nélkülözhetetlen az aktiválási entalpia és az aktiválási entrópia mennyiségi meghatározásához. Ezen képessége miatt az Eyring-egyenlet széles körben alkalmazható problémás esetek megoldására is a reakciókinetikában, főként a reakciósebességek meghatározásán keresztül. Jól ismert az aktiválási paraméterek közti összefüggés:

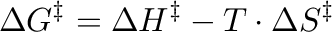$$\Delta G^{\ddag }=\Delta H^{\ddag } -T\cdot \Delta S^{\ddag }$$ (4.3)

Ha a 4.2 egyenlet mindkét oldalának vesszük a logaritmusát és behelyettesítjük az aktiválási entrópiát és entalpiát, akkor a következő egyenlethez jutunk:

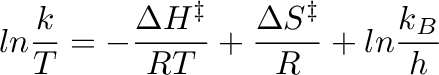$$ln \frac{k}{T}=-\frac{\Delta H^{\ddag }}{RT}+\frac{\Delta S^{\ddag }}{R}+ln\frac{k_B}{h} ~$$ (4.4)

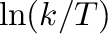Ha a reakciósebességet különböző hőmérsékleteken megmérjük és az $\ln(k/T)$ változót 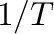$1/T$ függvényében ábrázoljuk, akkor egy egyenest kapunk, melynek meredekségéből meghatározhatjuk az aktiválási entalpiát, a függőleges tengelyen kapott metszéspontból pedig az aktiválási entrópiát.

Mégsem Ment Töröl