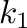Konszekutiv reakciók

A katalitikus ciklusok jellemzően több lépésből állnak, így a konszekutív modell (ha sokszor túlzott leegyszerűsítést is jelent) alkalmazható. A 4.16 egyenlet a legegyszerűbb esetet vázolja fel, amikor is a kiindulási anyagból (A) egy köztitermék (B) keletkezik, majd abból a termék (C). A két részlépést 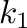$k_1$

és

sebességi állandókkal jellemezhetjük.

$\displaystyle \mathrm{A}\xrightarrow{k_1}\mathrm{B}\xrightarrow{k_2}\mathrm{C}$

(4.16)

Kezdeti feltételként (ha $t=0$

), rögzíthetjük, hogy $[\mathrm{A}]=[\mathrm{A}]_0$ , $[\mathrm{B}]=[\mathrm{C}]=0$ . A differenciálegyenlet-rendszer megoldása és a behelyettesítések után a három anyag koncentrációjára az alábbi egyenleteket kapjuk:

$\begin{equation*}\left.\begin{aligned}[\mathrm{A}]&=[\mathrm{A}]_0e^{-k_1t} \\ ... ...0}{k_2-k_1}(-k_2e^{-k_1t}+k_1e^{-k_2t})\end{aligned}\right\rbrace\end{equation*}$

Ha a reakciónkhoz még egy további lépést hozzáadunk, akkor már három sebességi állandóval kell számolnunk:

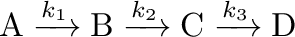$\displaystyle \mathrm{A}\xrightarrow{k_1}\mathrm{B}\xrightarrow{k_2}\mathrm{C}\xrightarrow{k_3}\mathrm{D}$

(4.18)

**4.2. Ábra:** Három lépésből álló konszekutiv reakciók koncentráció-idő profilja. A felső ábrán a harmadik, az alsónál a második lépés a sebességmeghatározó.
$\includegraphics[width=0.99\textwidth]{kinetika/abcd_peldak}$

A négyismeretlenes közönséges differenciálegyenlet-rendszer megoldása (itt nem részletezett módon) numerikusan történt, a négy komponens koncentrációjának időfüggése a 4.2 ábrán látható. A két koncentráció-idő profil összehasonlítása egy fontos jelenségre hívja fel figyelmünket, mely alapvető korlátot jelent bizonyos reakciók intermedierjeinek kísérleti úton történő tanulmányozásához. Ha ugyanis az utolsó részlépés a sebességmeghatározó, akkor elvileg a reakció intermedierjeit spektroszkópiai úton be lehet azonosítani. Ha azonban az első két lépés valamelyike a sebességmeghatározó lépés, akkor az “leárnyékolja” az összes többit. Az alsó példánál a B 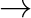$\rightarrow$ C lépés jóval lassabb, mint a zárólépés, így C intermediert gyakorlatilag nem látjuk az oldatban annak igen kis koncentrációja miatt.