A párhuzamos reakciók esetében az A kiindulási anyagból egyaránt keletkezik a B és a C anyag, ám a reakciósebességek (és azok sebességi állandói) eltérnek egymástól:
Kezdeti feltételek:
![$[\mathrm{A}]=[\mathrm{A}]_0; [\mathrm{B}]=[\mathrm{C}]=0$](img107.png)
Mind B, mind C keletkezésének sebességét ki tudjuk fejezni a kiindulási anyag koncentrációja (és persze a megfelelő sebességi állandók) segítségével:
Integrálás és egyszerűsítés után az alábbi nem túl bonyolult összefüggést kapjuk:
Azaz a két keletkező termék koncentráció-aránya megegyezik a hozzájuk tartozó sebességi állandók arányával. Természetesen ez akkor igaz, ha teljes mértékben kinetikai kontroll működik, azaz a 4.19 egyenletben szereplő mindkét reakció irreverzibilis. Ilyenkor a katalitikus reakciók szelektivitása is egyszerűen meghatározható.
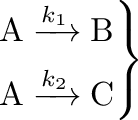
![$[\mathrm{A}]=[\mathrm{A}]_0; [\mathrm{B}]=[\mathrm{C}]=0$](img107.png)
![\begin{equation*}\left.\begin{aligned}\frac{d[\mathrm{B}]}{dt}&=k_1([\mathrm{A}]...
...mathrm{A}]_0-[\mathrm{B}]-[\mathrm{C}])\end{aligned}\right\rbrace\end{equation*}](img108.png)
![\begin{equation*}\left.\begin{aligned}[\mathrm{A}]&=[\mathrm{A}]_0e^{-(k_1+k_2)t...
...d}\right\rbrace \frac{[\mathrm{B}]}{[\mathrm{C}]}=\frac{k_1}{k_2}\end{equation*}](img109.png)