![\includegraphics[width=0.99\textwidth]{ligands/pdonortipusok}](img35.png)
|
A foszfinok3.1 (PR3), foszfitok (P(OR)3) és egyéb P-donor ligandumok kulcsszerepet töltenek be a különféle átmenetifémek (TM) által katalizált homogénkatalitikus reakciókban.Kollár and Keglevich [2010], Hartwig and Collman [2010], McAuliffe [1973], Tolman [1977], Jover et al. [2010,2012] A ligandumok helyes megválasztásával, azok változtatásával az átmenetifém komplexek katalitikus tulajdonságai jelentős mértékben befolyásolhatók. Ilyen jellemző például a fémkomplex katalízis során mutatott aktivitása, melyet alapvetően határoznak meg a fémhez koordinált ligandumok sztérikus és elektronikus tulajdonságai.Brown and Lee [1993], de Vries and Lefort [2006], Dias et al. [1994], Kühl [2005], Kamer et al. [2001] A P-donor ligandumok alaptípusait a 3.4 ábra mutatja be.
![\includegraphics[width=0.99\textwidth]{ligands/pdonortipusok}](img35.png)
|
A ligandumokon keresztül az aktivitáson túl a kemo-, regio-, és enantioszelektivitás növelésére is számos példát találunk.van Leeuwen et al. [2010], Colacot [2003], Kégl and Kollár [2013], Botteghi et al. [1991], Knowles [2002], Hayashi [2000], Fernández-Pérez et al. [2011], Lefort et al. [2004], Minnaard et al. [2007], Hoen et al. [2004] Régóta ismert, hogy a ligandumon található szubsztituenseken keresztül a ligandumokon kívül azok fémekhez való koordinációs sajátságai is változtathatók. A komplexeken belül ezért a fém-foszfor kölcsönhatás karakterizálása kulcsfontosságú a katalitikus hatás megértése és a katalizátortervezés szempontjából, ezért a ligandumok kvantitatív és kvalitatív kategorizálásának igénye már igen korán megjelent.
Strohmeier és munkatársai az 1960-as években különféle ligandumtípusok (nitrilek, izonitrilek, szulfoxidok, foszfinok) 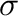 -donor és
-donor és 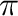 -akceptor sajátságait vizsgálták.Strohmeier and Müller [1967] A CpMn(CO)2L, CpV(CO)3L, Fe(CO)4L és Ni(CO)3L (Cp=C5H5) komplexek közös vonása, hogy karbonil ligandumokat is tartalmaznak, így a karbonil vegyértékrezgések változásán keresztül a foszfinokat további négy kategóriába sorolták. A vizsgált frekvenciatartomány a négy komplexre rendre 1927-1996, 1946-1982, 2045-2101 és 2060-2110 cm-1 volt.
-akceptor sajátságait vizsgálták.Strohmeier and Müller [1967] A CpMn(CO)2L, CpV(CO)3L, Fe(CO)4L és Ni(CO)3L (Cp=C5H5) komplexek közös vonása, hogy karbonil ligandumokat is tartalmaznak, így a karbonil vegyértékrezgések változásán keresztül a foszfinokat további négy kategóriába sorolták. A vizsgált frekvenciatartomány a négy komplexre rendre 1927-1996, 1946-1982, 2045-2101 és 2060-2110 cm-1 volt.
Jelentős mértékben Strohmeier tanulmányaira alapozva Tolman az 1970-es években a Ni(CO)3(monofoszfin) komplexekre alapozva új rendszert állított fel. Hetven L=PR1R2R3 általános képlettel jellemezhető foszfin elektronikus hatását vizsgálta meg az A karbonil vegyértékrezgések összehasonlításával.Tolman [1970,1977] Úgy találta, hogy a foszforon lévő funkciós csoportok hatásai külön-külön értelmezhetők és azok együttes hatása alakítja ki hatását a CO rezgésre. A hozzájárulások a
karbonil vegyértékrezgések összehasonlításával.Tolman [1970,1977] Úgy találta, hogy a foszforon lévő funkciós csoportok hatásai külön-külön értelmezhetők és azok együttes hatása alakítja ki hatását a CO rezgésre. A hozzájárulások a  (cm
(cm ) jelölést kapták, és a leginkább bázikus ligandum, a (tri-terc-butil-foszfin), mely a legerősebb
) jelölést kapták, és a leginkább bázikus ligandum, a (tri-terc-butil-foszfin), mely a legerősebb 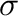 -donor és a leggyengébb
-donor és a leggyengébb 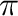 -akceptor, volt kijelölve a skála egyik végpontjának (3.1. egyenlet).
-akceptor, volt kijelölve a skála egyik végpontjának (3.1. egyenlet).

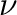 (CO) rezgésről szoktak beszélni, ilyen szigorúan véve csak a PH3 és PMe3 ligandumokat tartalmazó Ni-karbonil komplexekben van, melyek valóban C3v szimmetriával rendelkeznek. Így például a C3 szimmetriájú Ni(CO)3(PPh3) komplex esetén, már csak A rezgésről lehetne beszélni.
(CO) rezgésről szoktak beszélni, ilyen szigorúan véve csak a PH3 és PMe3 ligandumokat tartalmazó Ni-karbonil komplexekben van, melyek valóban C3v szimmetriával rendelkeznek. Így például a C3 szimmetriájú Ni(CO)3(PPh3) komplex esetén, már csak A rezgésről lehetne beszélni.
A NiL(CO)3 komplexhez tartozó vegyértékrezgések, vagyis a TEP (Tolman-féle elektronikus paraméter) jól korreláltatható a Strohmeier-féle CpMnL(CO)3 rendszerrel (3.2. egyenlet).Kühl [2005], Strohmeier and Müller [1967]
Noha ezen könyv keretei között nem foglalkozunk elektronszerkezeti módszerekkel, egy olyan eredményt mégis bemutatunk, ami a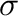 -donor foszfinok karbonil ligandumokra gyakorolt hatását szemlélteti elég látványos módon (3.6 a. ábra). Az ábra egy, a Ni(CO)3(PMe3) komplexen végrehajtott EDA-NOCV (energiadekompozíciós analízis a természetes vegyértékpályákon) eredménye, ahol a deformációs sűrűség (
-donor foszfinok karbonil ligandumokra gyakorolt hatását szemlélteti elég látványos módon (3.6 a. ábra). Az ábra egy, a Ni(CO)3(PMe3) komplexen végrehajtott EDA-NOCV (energiadekompozíciós analízis a természetes vegyértékpályákon) eredménye, ahol a deformációs sűrűség (
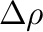 : az az elektronsűrűség különbség, amit akkor kapunk ha a komplex teljes elektronsűrűségből kivonjuk a fragmensekre bontott komplex elektronsűrűségét)
: az az elektronsűrűség különbség, amit akkor kapunk ha a komplex teljes elektronsűrűségből kivonjuk a fragmensekre bontott komplex elektronsűrűségét) 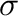 -donor kölcsönhatásra eső komponensét jelenítjük meg vizuálisan. A színkódok figyelembe vételével (az arany szín azt mutatja meg honnan indul, a zöld azt, hova érkezik az elektronsűrűség) jól látható az egész elvnek a lényege: a foszfor mint Lewis-bázis, a magános párjáról a fémen keresztül elektronsűrűséget ad át, az összes karbonil ligandumnak, azok lazító pályáin növelvén az elektronsűrűséget. A lazító pályán megnövelt populáció kisebb kötésrendhez, az kisebb erőállandóhoz vezet, aminek eredménye az alacsonyabb hullámszámnál jelentkező
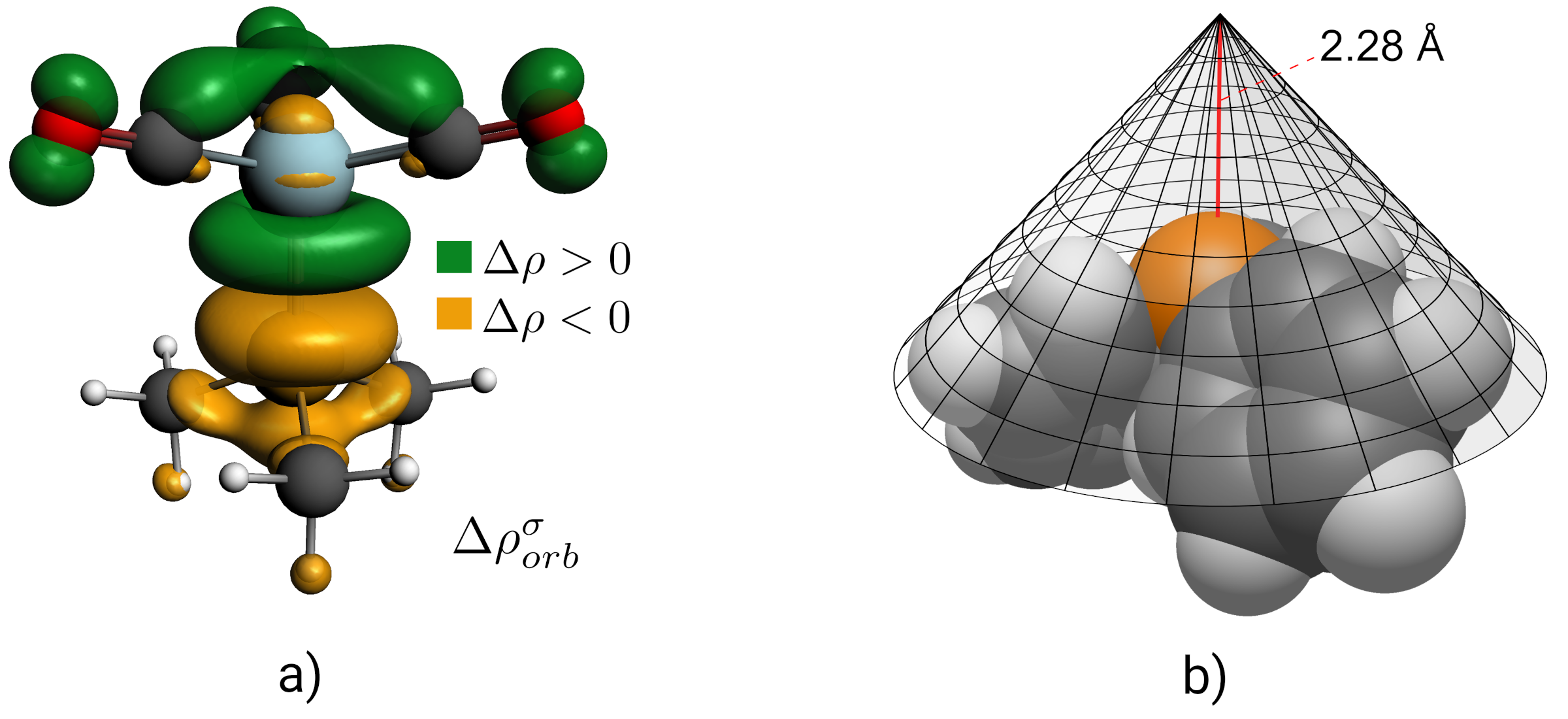
-donor kölcsönhatásra eső komponensét jelenítjük meg vizuálisan. A színkódok figyelembe vételével (az arany szín azt mutatja meg honnan indul, a zöld azt, hova érkezik az elektronsűrűség) jól látható az egész elvnek a lényege: a foszfor mint Lewis-bázis, a magános párjáról a fémen keresztül elektronsűrűséget ad át, az összes karbonil ligandumnak, azok lazító pályáin növelvén az elektronsűrűséget. A lazító pályán megnövelt populáció kisebb kötésrendhez, az kisebb erőállandóhoz vezet, aminek eredménye az alacsonyabb hullámszámnál jelentkező 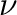 (CO) rezgés.Kégl et al. [2016]
(CO) rezgés.Kégl et al. [2016]
|
A TEP skála segítségével azonban kelátképző ligandumok, például difoszfinok, már nem értelmezhetők. Crabtree és munkatársai a kétmagvú ligandumok leírására is alkalmas modellvegyületet javasoltak. A MoL2(CO)4 komplexek (L2: egy kétfogú vagy két egyfogú foszfin ligandum) CO vegyértékrezgéseiből egy univerzálisabban alkalmazható elektronikus paramétert vezettek be.Anton and Crabtree [1983] Tizenegy, a TEP skálát lefedő monofoszfinnal szintetizálták a megfelelő molibdén-karbonil komplexeket és megállapították, hogy a kétféle elektronikus paraméter skála között erős lineáris korreláció áll fenn (3.3. egyenlet). Ebből, és a Strohmeier skálából is egyre inkább az a tapasztalati összefüggés kezdett körvonalazódni, hogy az átmenetifém karbonil komplexekben kimutatható elektronikus hatások “kompatibilisek” egymással, vagyis a hatás szinte független az adott karbonil-komplex típusától.
A difoszfinok kategorizálásának lehetőségét kibővítettük két újabb modellvegyülettel (Pd(PP)(CO), HRh(PP)(CO)), ahol PP egy difoszfint, vagy két monofoszfint jelöl), melyek katalitikus szempontból jelentőséggel bírnak, de nagy reakcióképességük miatt csak a számításos kémia segítségével vizsgálhatók (ilyenkor az elektronikus paramétert TEP helyett CEP-nek szoktuk jelölni).Kégl et al. [2018] A számított regressziós paraméterekre rendre 0,985 és 0,987 értékeket kaptunk és a kísérleti TEP paraméterekhez viszonyítva az alábbi egyenleteket:
![\includegraphics[width=1.05\textwidth]{ligands/diphosphines}](img49.png)
|
Noha a TEP skála a katalízishez köthető foszfinkémiában széles körben elfogadott, nem árt megemlíteni a módszer néhány hiányosságát is. A ligandum koordináció során mutatott tulajdonságait a 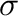 -donor és
-donor és 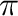 -akceptor tulajdonságok együttesen határozzák meg, míg a TEP, és az összes ugyanazon elvre épülő módszer csak a nettó donor erőt veszi figyelembe. Néhány esetben a karbonil vegyértékrezgéseket a téren keresztül kialakuló gyenge kölcsönhatások is befolyásolják, mint ahogy ezt Sierra és munkatársai leírták mangán-félszendvics komplexek esetében.Valyaev et al. [2011] Lineáris arany-karbonil komplexeknél a nikkel karbonil komplexekhez képest alapvetően eltérő viselkedést tapasztaltak, itt ugyanis a ligandum donor erőssége helyett az aranyról a ligandumra történő viszontkoordináció befolyásolta a karbonil rezgéseket.Ciancaleoni et al. [2014]
-akceptor tulajdonságok együttesen határozzák meg, míg a TEP, és az összes ugyanazon elvre épülő módszer csak a nettó donor erőt veszi figyelembe. Néhány esetben a karbonil vegyértékrezgéseket a téren keresztül kialakuló gyenge kölcsönhatások is befolyásolják, mint ahogy ezt Sierra és munkatársai leírták mangán-félszendvics komplexek esetében.Valyaev et al. [2011] Lineáris arany-karbonil komplexeknél a nikkel karbonil komplexekhez képest alapvetően eltérő viselkedést tapasztaltak, itt ugyanis a ligandum donor erőssége helyett az aranyról a ligandumra történő viszontkoordináció befolyásolta a karbonil rezgéseket.Ciancaleoni et al. [2014]
Az elektronikus paraméterek mellett Tolman a sztérikus hatás kategorizálása terén is úttörőnek bizonyult. Az általa megtervezett rendszer mechanikus CPK modellen alapult; a megépített szerkezetekre illesztett kúpszög adta meg az adott ligandum sztérikus paramétereit (3.6 ábra, b.). A kúp úgy kerül kialakításra, hogy a donoratom (legtöbb esetben foszfor) és a kúp csúcsa között 2,28 Å (azaz 228 pm) a távolság. Azoknál a ligandumoknál, ahol több konformerrel kell számolni, ott a szubsztituenseket úgy állította be, hogy a térkitöltés minimális legyen.Tolman [1977]
A kúpszög (jelölése általában
 ) kiszámításának egy kézenfekfő módja a ligandum röntgenszerkezete alapján történő meghatározásSnelders et al. [2011]. Ahol ez nem lehetséges, ott jól használható a Bartik és munkatársai által talált érdekes összefüggés. A kérdéses ligandum transz-[PdCl2L2] komplexének 31P NMR kémiai eltolódása ugyanis jó korrelációt ad a Tolman-féle kúpszöggel (3.6. egyenlet).Bartik and Himmler [1985], Bartik et al. [1993]
) kiszámításának egy kézenfekfő módja a ligandum röntgenszerkezete alapján történő meghatározásSnelders et al. [2011]. Ahol ez nem lehetséges, ott jól használható a Bartik és munkatársai által talált érdekes összefüggés. A kérdéses ligandum transz-[PdCl2L2] komplexének 31P NMR kémiai eltolódása ugyanis jó korrelációt ad a Tolman-féle kúpszöggel (3.6. egyenlet).Bartik and Himmler [1985], Bartik et al. [1993]
Mivel a kémiai eltolódás egyértelműen a foszforatom körüli elektronsűrűségtől függ, ezért kísérleti úton is megállapítható, hogy a sztérikus és elektronikus paraméterek nem függetlenek egymástól.
Néhány gyakoribb P-donor foszfin és foszfit elektronikus és sztérikus Tolman-paraméterét a 3.2 táblázat foglalja össze.